Diferença entre covariância e correlação

A covariância e a correlação são conceitos estatísticos essenciais para quem deseja compreender melhor como duas variáveis se relacionam. Enquanto a covariância mostra se elas caminham na mesma direção ou em sentidos opostos, a correlação vai além e mede a intensidade desse vínculo.

Neste texto, a gente fala mais sobre isso. Vamos lá?

O que é covariância?

A covariância é um conceito estatístico que ajuda a entender como duas variáveis se comportam em relação uma à outra. Ela funciona como uma régua que mede se há algum tipo de ligação entre elas e qual o sentido dessa relação.

Quando a covariância é nula, isso indica que não existe associação perceptível entre os dados analisados. Já quando o valor é positivo, mostra que as variáveis tendem a caminhar na mesma direção: se uma cresce, a outra também tende a crescer.

Por outro lado, se a covariância é negativa, o movimento acontece de forma contrária, ou seja, o aumento de uma variável costuma vir acompanhado da queda da outra.

Esse tipo de análise é muito utilizado em estatística, economia e até no mercado financeiro, já que permite observar como determinados fatores se relacionam.

Afinal, compreender essas interdependências pode ajudar a prever comportamentos e tomar decisões com mais segurança e embasamento.

Como calcular a covariância?

A fórmula que a gente usa para calcular a covariância é:

Σ ( xi – xmed ) ( yi – ymed ) / ( n – 1 )

Na fórmula, cada símbolo representa o seguinte:

• Σ: indica o somatório de todos os itens da fórmula.
• xi: o valor de x na posição i, sendo i o índice correspondente.
• x̄ (xmed): representa a média de todos os valores de x no conjunto de dados.
• yi: o valor de y na posição i, onde i indica o índice.
• ȳ (ymed): corresponde à média de todos os valores de y no conjunto de dados.
• n: total de itens no conjunto de dados.

O cálculo da covariância pode ser feito em etapas simples:

1. Conheça a fórmula e organize os dados: reúna os valores dos dois ativos (ou variáveis) que você deseja analisar em uma tabela, alinhando-os sempre pela mesma referência, como datas ou períodos iguais.
2. Calcule a média de cada variável: para encontrar a média de X (x̄) e de Y (ȳ), some todos os valores de cada variável e divida pela quantidade de observações.
3. Encontre os desvios em relação à média: subtraia a média de cada valor: (xi – x̄) para X e (yi – ȳ) para Y. Esses desvios podem ser positivos ou negativos, dependendo se o valor está acima ou abaixo da média.
4. Multiplique os desvios correspondentes: para cada posição, multiplique (xi – x̄) pelo (yi – ȳ).
5. Some os resultados: depois de multiplicar todos os pares, some os valores obtidos.
6. Aplique o denominador: divida essa soma pelo número de observações menos 1 (n – 1).

O valor final será a covariância, que mostra como os dois ativos variam em conjunto: positiva quando tendem a se mover na mesma direção e negativa quando se movem em direções opostas.

Como interpretar a covariância?

Para interpretar esse conceito de forma prática, é fundamental observar alguns cenários:

Covariância positiva

Quando o valor é positivo, significa que as variáveis tendem a seguir a mesma direção. Por exemplo: se uma aumenta, a outra também tende a aumentar.

É o que acontece, por exemplo, com horas de estudo e notas em provas, em geral, quanto mais tempo dedicado, melhores os resultados.

Covariância negativa

Nesse caso, as variáveis caminham em sentidos opostos. Ou seja, quando uma cresce, a outra diminui. Um exemplo simples é o preço de um produto e a quantidade comprada: se o preço sobe muito, a tendência é que as pessoas comprem menos.

Covariância igual a zero

Quando o resultado é próximo de zero, isso indica que não existe uma relação linear relevante entre as variáveis. Isso não significa que não haja nenhuma ligação, mas sim que ela não segue um padrão direto de aumento ou queda.

Outro ponto importante é que a covariância não padroniza a intensidade da relação. Isso porque o valor calculado depende diretamente das unidades de medida das variáveis.

Assim, interpretar o número exato pode ser difícil, ele só mostra a direção da relação, não o “quão forte” ela é. Por isso, em muitos casos, os analistas preferem usar o coeficiente de correlação, que é derivado da covariância, mas padronizado em uma escala de -1 a 1, facilitando a comparação.

O que é correlação?

A correlação é um recurso estatístico que mede o grau de relacionamento entre duas variáveis, mostrando se existe uma ligação entre elas e qual a intensidade dessa relação.

Diferente da covariância, que apenas indica o sentido do movimento conjunto, a correlação vai além: ela mostra o quanto essa relação é forte ou fraca, sempre dentro de uma escala que varia de -1 a +1.

Quando o valor da correlação se aproxima de +1, significa que as variáveis tendem a se mover juntas na mesma direção, de forma bastante alinhada.

Já próximo de -1, a relação é inversa: enquanto uma aumenta, a outra geralmente diminui. Valores perto de 0 indicam pouca ou nenhuma associação significativa entre elas.

No mundo dos investimentos, por exemplo, a correlação é uma ferramenta essencial para entender como dois ativos se comportam em conjunto. Isso ajuda a avaliar riscos e a buscar estratégias de diversificação mais precisas.

Como calcular a correlação?

A fórmula de produto-momento de Pearson é a que vamos usar:

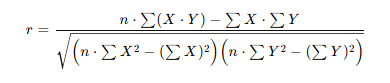
Imagine que um professor deseja verificar se existe relação entre o número de horas que seus alunos estudaram e as notas obtidas em uma prova. Para simplificar, vamos considerar três alunos.

O primeiro estudou 2 horas e tirou 60 pontos, o segundo estudou 4 horas e ficou com 70 pontos, enquanto o terceiro dedicou 6 horas e alcançou 90 pontos.

Com esses dados, é possível aplicar a fórmula da correlação de Pearson. Primeiro, somam-se os valores de cada variável: as horas de estudo somam 12 e as notas, 220.

Em seguida, calcula-se a soma dos produtos entre cada par de valores, que resulta em 940.

Também é necessário encontrar a soma dos quadrados: para as horas de estudo, o valor é 56, e para as notas, 16.600.

Agora, aplicando na fórmula o numerador:

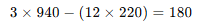
Já o denominador:

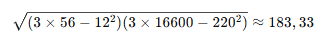
Dividindo o numerador pelo denominador, chegamos a um coeficiente de correlação de aproximadamente 0,98. Esse resultado, inclusive, indica uma correlação positiva muito forte, ou seja, quanto mais os alunos estudaram, maiores foram as suas notas.

Como interpretar a correlação?

Interpretar a correlação significa analisar o valor do coeficiente de correlação, que normalmente varia entre -1 e +1. Esse número é como um termômetro da relação, digamos assim, entre duas variáveis, indicando se elas caminham juntas, em direções opostas ou se praticamente não têm ligação.

• Próximo de +1: revela uma correlação positiva forte, ou seja, quando uma variável cresce, a outra tende a crescer também.
• Próximo de -1: indica uma correlação negativa forte, mostrando que, quando uma sobe, a outra geralmente cai.
• Perto de 0: sugere que não há uma relação linear significativa entre os dados analisados.

Diante disso, vale destacar que esse coeficiente apenas o grau de associação linear. Isso significa que ele mostra se existe um movimento conjunto, mas não quer dizer que uma variável cause a mudança da outra.

Qual a diferença entre covariância e correlação?

Embora estejam sempre lado a lado nos estudos estatísticos, covariância e correlação não são exatamente a mesma coisa. A covariância mostra se duas variáveis se movem juntas (no mesmo sentido ou em sentidos opostos), mas o seu valor depende diretamente da escala das variáveis analisadas.

Isso significa que, dependendo das unidades usadas, como reais, dólares, metros ou quilos, o resultado da covariância pode variar bastante, o que às vezes dificulta a interpretação.

Já a correlação é uma espécie de versão padronizada da covariância. Ela traduz essa relação para uma escala fixa, que vai de -1 a +1, facilitando a comparação entre diferentes situações.

Dessa forma, independentemente da unidade de medida, é possível identificar não só o sentido, mas também a intensidade da relação entre as variáveis.

Importância da covariância e da correlação nos investimentos

Quando a gente parte para a categoria de investimentos, tanto a covariância quanto a correlação são ferramentas muito importantes para quem busca montar uma carteira equilibrada e reduzir riscos.

Afinal, essas medidas ajudam a entender como diferentes ativos se comportam em conjunto, o que é essencial quando o objetivo é diversificar.

A covariância, nesse contexto, mostra a direção da relação entre os ativos: se eles tendem a se mover juntos ou em sentidos opostos. Já a correlação vai mais adiante, padronizando esse resultado em uma escala que facilita a comparação e permite avaliar a intensidade dessa relação.

Portanto, ao serem usadas em conjunto, essas métricas facilitam a gestão de riscos. Elas ajudam o investidor a evitar a concentração excessiva em ativos que se movem de forma semelhante, e a buscar combinações que realmente tragam equilíbrio à carteira.

Afinal, a ideia da diversificação não é apenas ter vários ativos, mas sim escolher aqueles que se complementam e tornam os resultados menos vulneráveis às oscilações do mercado.

• Leia também: Descorrelação: o que é, como funciona, importância

Fonte: Psicomentria Online, Top Invest, Mais Retorno, Investopedia.